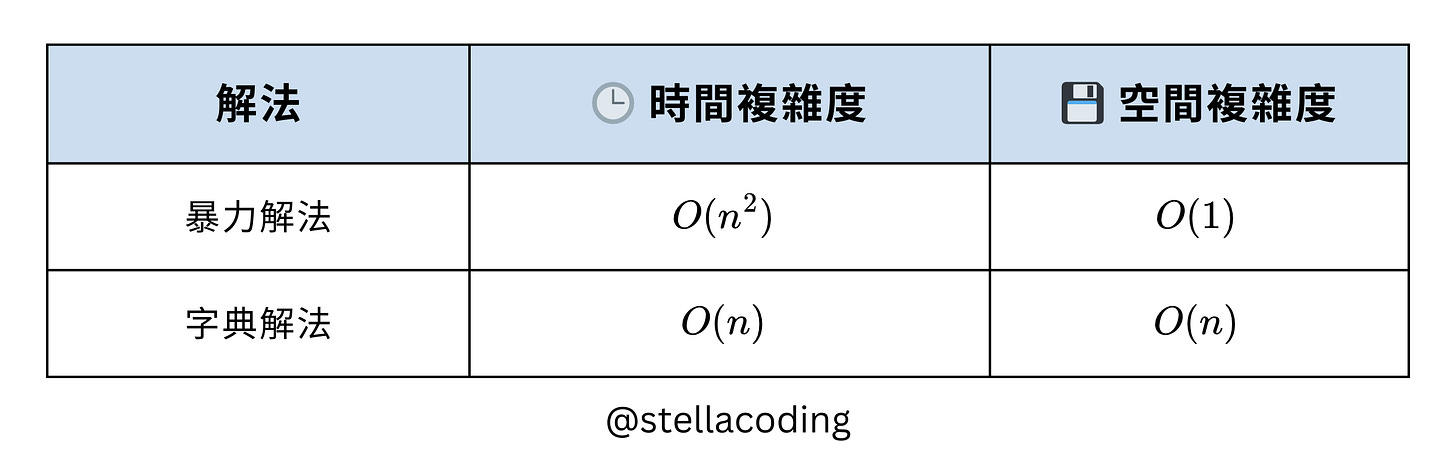
在本系列文章中，說明了不同 LeetCode 題型的時間與空間複雜度分析。而本篇將以最經典的入門題目 Two Sum 為例，再次說明兩種核心解法: 暴力解法與字典解法，並比較時間與空間的權衡取捨。
暴力解法
時間複雜度 O(n2)
空間複雜度 O(1)
class Solution(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
for i in range(len(nums)):
for j in range(i+1, len(nums)):
if nums[i]+nums[j]==target:
return [i,j]
nums = [2,7,11,15]
target = 9
Solution().twoSum(nums, target) #[0, 1]分析複雜度
時間複雜度是 O(n²)
當 i=0 → j 從 1 到 n-1，要跑 n-1 次
當 i=1 → j 從 2 到 n-1，要跑 n-2 次
…
當 i=n-2 → j 只剩 n-1，要跑 1 次
當 i=n-1 → j 沒有值，要跑 0 次
總執行次數 = (n-1) + (n-2) + … + 1 = n(n-1)/2 ≈ O(n²)
所以時間複雜度 = O(n²)
空間複雜度是 O(1)
只用了幾個變數: `i`、`j` 和`list [i, j]`
沒有使用與輸入規模 n 成長相關的額外資料空間
所以空間複雜度 = O(1)
字典解法
時間複雜度 O(n)
空間複雜度 O(n)
class Solution(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
d = {}
for i,v in enumerate(nums):
diff=target-v
if diff in d:
return [d[diff],i]
d[v]=i
nums = [2,7,11,15]
target = 9
Solution().twoSum(nums, target) #[0, 1]分析複雜度
時間複雜度是 O(n)
迴圈跑 n 次 `(n = len(nums))` → O(n)
每次迭代內的操作:
計算 `diff = target - v` → O(1)
查詢 `diff in d` → O(1)
插入 `d[v] = i` → O(1)
所以時間複雜度 = O(n)
空間複雜度是 O(n)
只用了幾個變數: `i`、`v`、`diff`
使用了一個字典 d → O(n)
所以空間複雜度 = O(n)
時間 vs 空間
用Two Sum比較兩種核心解法的複雜度。
這個對比說明了演算法設計中最常見的取捨，我們用了額外的線性記憶體空間，從而「換取」時間複雜度從平方級降到線性級的顯著提升。
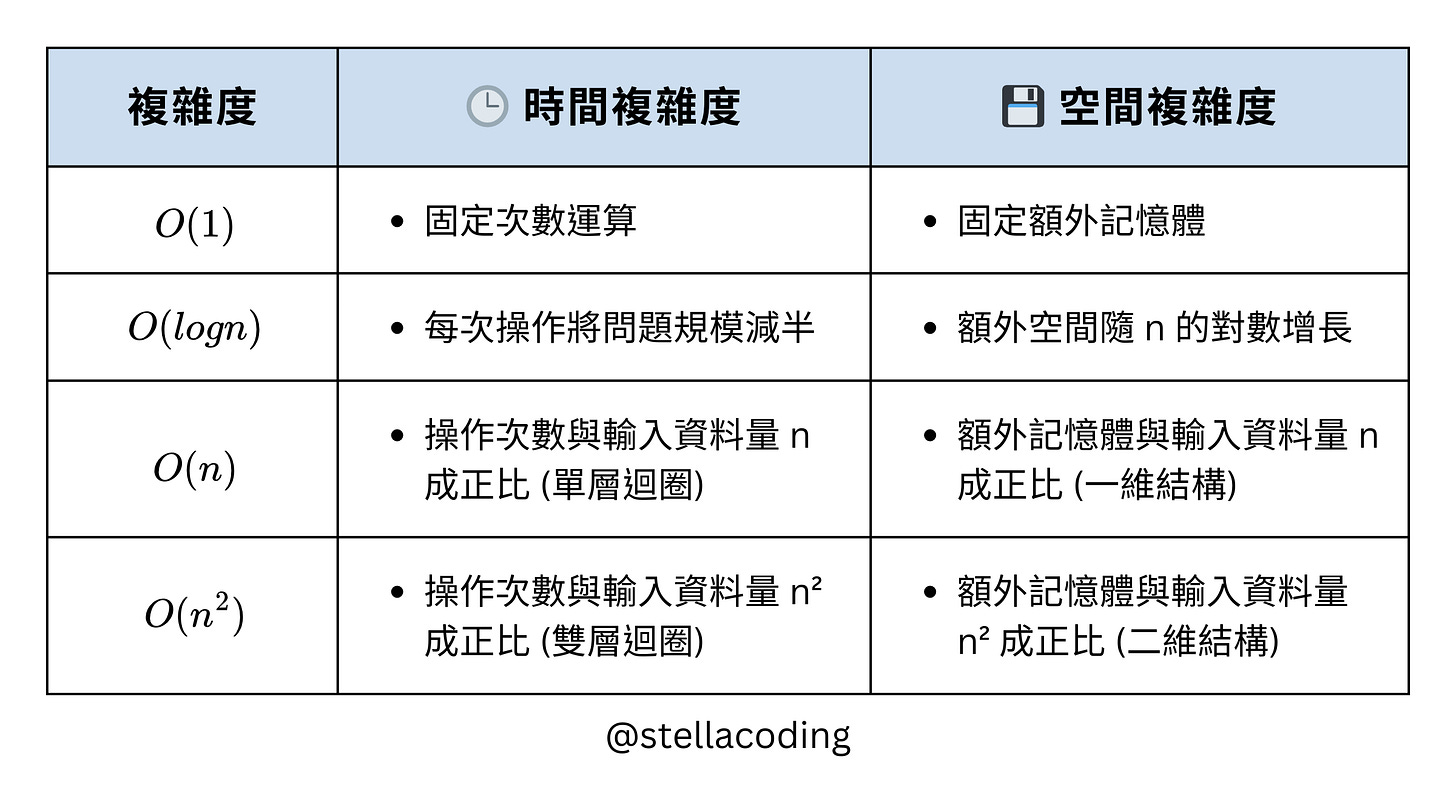
複雜度速查表
常見QA
Q: 沒有迴圈就是 O(1) 嗎？
A: 不一定。如果迴圈次數是「固定常數」，例如`for i in range(100)`，時間仍是 O(1)。但若呼叫一個需要處理 n 筆資料的函式，即使沒有顯式迴圈，也可能是 O(n)。
Q: 空間複雜度要把輸入也算進去嗎？
A: 一般空間複雜度計算的是「額外」空間，輸入參數所占用的空間通常是不計入的。
Q: 若 Big-O 有常數項呢？
A: 複雜度關注的是成長趨勢，而不是絕對的執行時間或記憶體用量，故係數和常數項通常被忽略，例如 O(2n) 視為 O(n)。