三角形成立條件

為什麼是「兩邊和大於第三邊」?

你有想過三角形為什麼是「兩邊和大於第三邊」嗎?

在幾何學中，並非任意三條線段都能組成一個三角形。

要構成一個真正的三角形，必須滿足一個基本條件:

任意兩邊之和必須大於第三邊。

而這就是 「三角形不等式定理(Triangle Inequality Theorem)」。

兩點之間直線最短

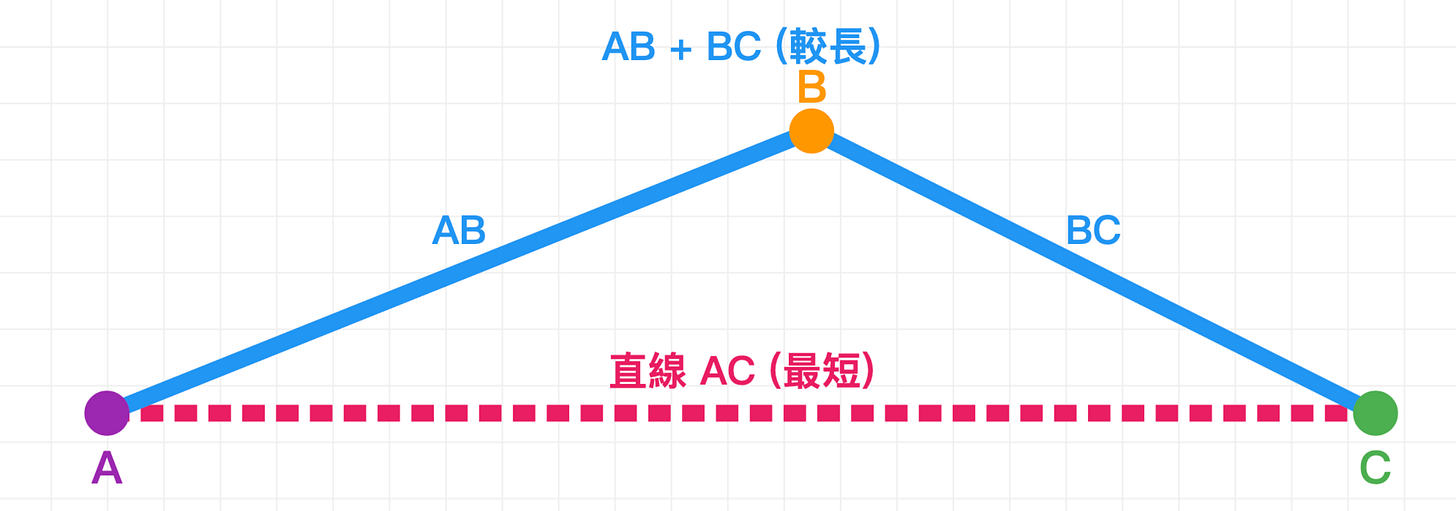
在平面幾何中，給定兩點 A 和 C:

• A 和 C之間的最短距離是 AC。

• 若你從 A 出發，先到另一點 B ，再抵達 C ，則路徑長度為 AB+BC。

• 因此我們可以得知 AC ≤ AB + BC

這就是「兩點之間直線最短」原則。

三角形不等式

考慮三角形 △ABC，三邊長分別是:

a = AB, b = BC, c = AC

根據「兩點最短路徑」原理，我們可以得出三個不等式:

a + b > c → AB + BC > AC
b + c > a → BC + AC > AB
a + c > b → AB + AC > BC

這就是完整的三角形不等式，換句話說，「任意兩邊之和 > 第三邊」。

為什麼不是「≤」?

小於的情況

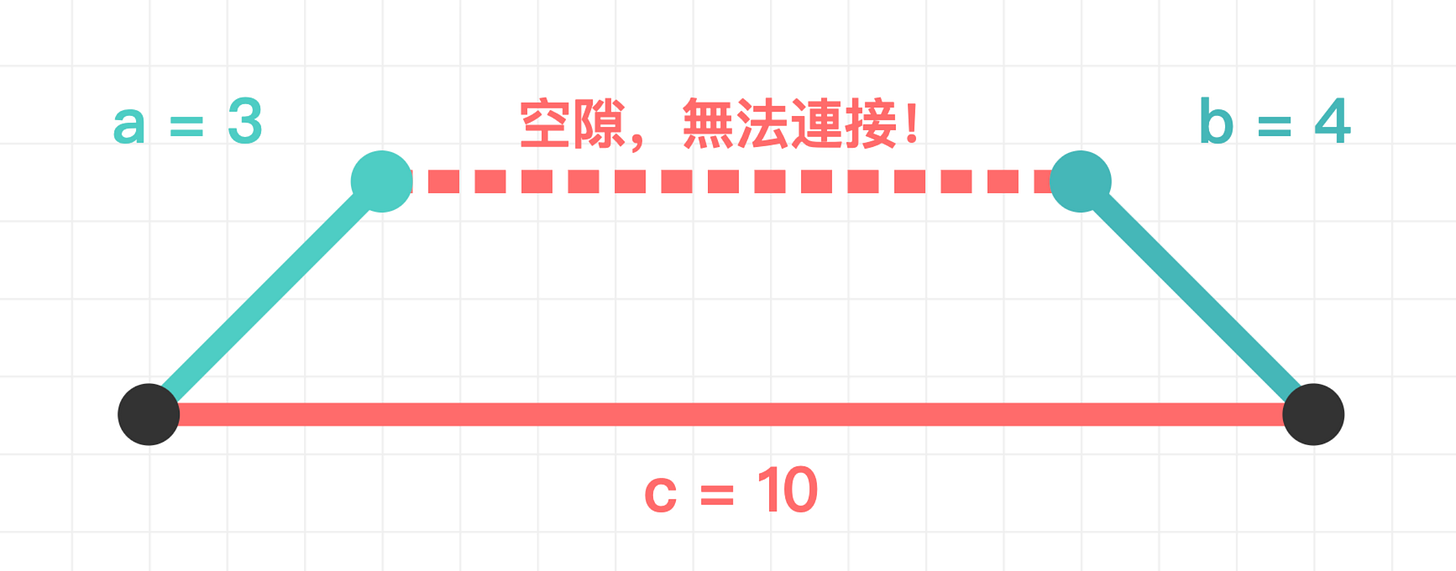
• 若 a + b < c、b + c < a、a + c < b

• 兩邊加起來比第三邊短，怎麼都連不起來，自然無法形成封閉圖形。

範例: a=3, b=4, c=10 → a+b=7 < 10

等於的情況

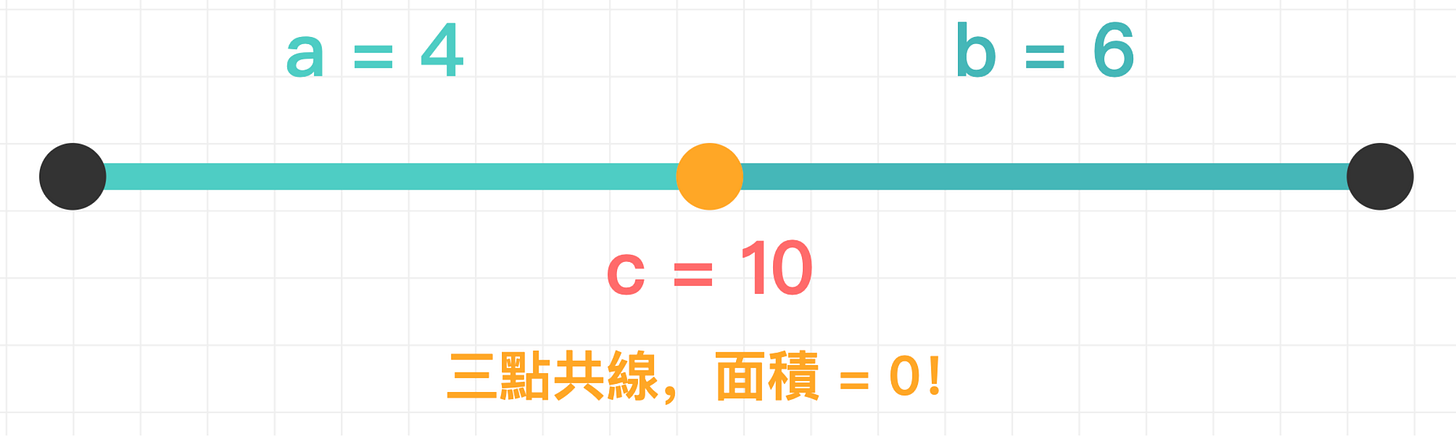
• 若 a + b = c、b + c = a、a + c = b

• 三個點會落在同一直線上，三角形退化成一條線段，面積 = 0，不算三角形。

範例: a=4, b=6, c=10 → a+b=10 = 10

大於的情況

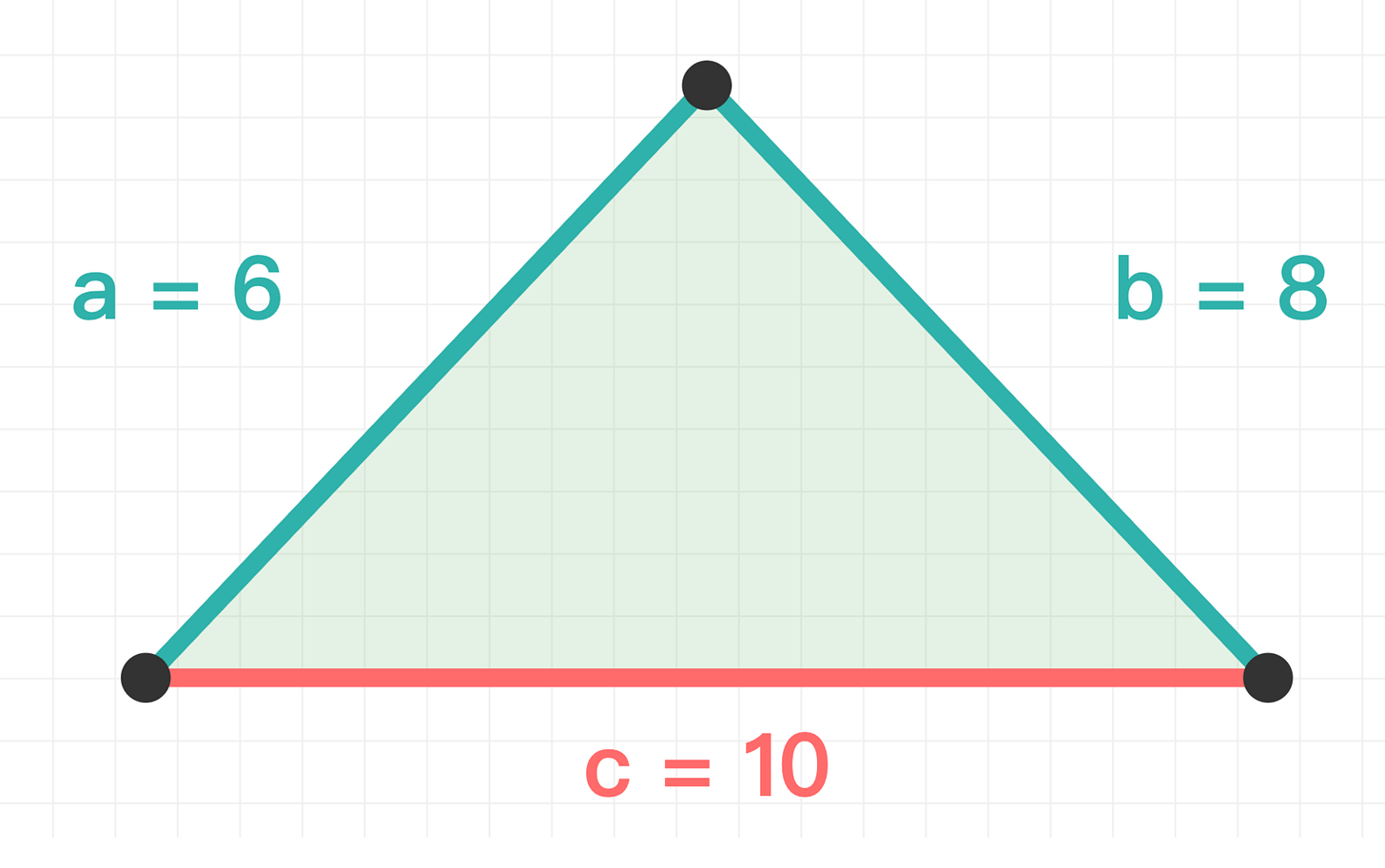
• 若 a + b > c、b + c > a、a + c > b

• 三邊才能首尾相接，形成一個真正有面積的三角形。

範例: a=6, b=8, c=10 → a+b=14 > 10

總結

三角形成立的必要條件是:

• 兩邊和 < 第三邊 → 無法封閉，無法形成三角形。

• 兩邊和 = 第三邊 → 退化為直線，面積 = 0。

• 兩邊和 > 第三邊 → 能形成真正的三角形。

也因此，三角形不等式是「任意兩邊之和必須大於第三邊」。